Wir bieten dir hier eine kurze Wiederholung und Zusammenfassung der wichtigsten Inhalte für die Mathe Prüfung im MSA oder EBBR.
In der MSA Matheprüfung werden dabei viele verschiedene Gebiete der Mathematik abgefragt. Themengebiete aus der siebten und achten Klasse, wie lineare Gleichungen, sind ebenso vertreten wie die Exponentialfunktionen, die zum Stoff der zehnten Klasse gehören.
Über die Prüfung
Die Vorbereitung und aufgelisteten Themen eignen sich für
- den Mittleren Schulabschluss (MSA)
- die erweiterte Berufsbildungsreife (eBBR)
in Berlin sowie
- die Fachoberschulreife (FOR) nach der 10. Jahrgangsstufe
- die erweiterte Berufsbildungsreife (EBR)
in Brandenburg.
Natürlich kannst du die Zusammenfassung ebenfalls nutzen, um allgemein die Inhalte der 7. bis 10. Klasse im Fach Mathematik zu wiederholen.
Zusammenfassung wichtiger Mathe-Inhalte
Für ausführliche Erklärungen und Übungen zu den Themen der 7. bis 10.Klasse sowie der Oberstufe empfehlen wir die MatheWiki-App für Android oder iOS. Die hier aufgeführten Themen sind nur ein kleiner Auszug aus den relevanten Inhalten.
Lineare Gleichungen
Lineare Gleichungen kann man mit Hilfe von Äquivalenzumformung lösen. Das erreicht man, indem man sie nach x auflöst.
Bei der Umformung darf sich die Lösungsmenge der Gleichung nicht verändern.
Das erreichst Du durch:
- das Auflösen, Ordnen und Zusammenfassen von Klammern
- eine beidseitige Addition bzw. Subtraktion derselben Zahlen
- eine beidseitige Multiplikation bzw. Division mit derselben Zahl (Bedingung: Zahl ≠ 0)
Quadratische Gleichungen
Als eine quadratische Gleichung wird jede Gleichung bezeichnet, die man in die allgemeine Form ax²+bx+c=0 bringen kann. Voraussetzung ist aber, dass a≠0 ist.
- a, b und c sind Koeffizienten.
- Die Gleichung x²+px+q=0 heißt Normalform der quadratischen Gleichung. Es ist möglich jede quadratische Gleichung in die Normalform zu bringen.
- Gleichungen in der Form x²+q=0 nennt man rein quadratisch.
- Gemischt quadratisch sind Gleichungen mit der Form x²+px+q=0. Eine quadratische Gleichung kann entweder eine, zwei oder keine Lösungen haben.
Quadratische Gleichungen lassen sich mit der pq-Formel lösen. Dies wird zum Beispiel zum Berechnen von Nullstellen benötigt.
Anwendung
Am Anfang braucht man die Normalform: x² + px + q=0
Die pq-Formel zum Lösen dieser Gleichung lautet: 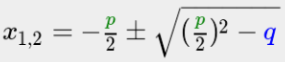
Hier ein Beispiel:

Lineare Funktionen
Jede lineare Funktion besitzt die allgemeine Funktionsgleichung: y = mx + n
Dabei bezeichnet m die Steigung der Geraden und n den y-Achsenabschnitt. Um die Steigung zu berechnen benötigt man zwei beliebige Punkte auf der Geraden.
P1 (x1| y1) und P2 (x2| y2)
Damit man nun m berechnen kann, muss die Differenz der x- und y-Werte der Punkte bestimmt werden.
Beispiel:
P1 (1| 2) und P2 (3| 6)
Δx= 6-2= 4
Δy= 3-1= 2
m= Δy : Δx= 4:2= 2
➜ Die Steigung der Geraden durch die Punkte P1 und P2 beträgt 2.
Satz des Pythagoras
Voraussetzung für die Satzgruppe des Pythagoras ist ein rechtwinkliges Dreieck.
Man unterscheidet die Katheten und die Hypotenuse
- Die Hypotenuse (hier BC) ist die längste Seite des Dreiecks.
- Als Katheten werden die übrigen Seiten bezeichnet.
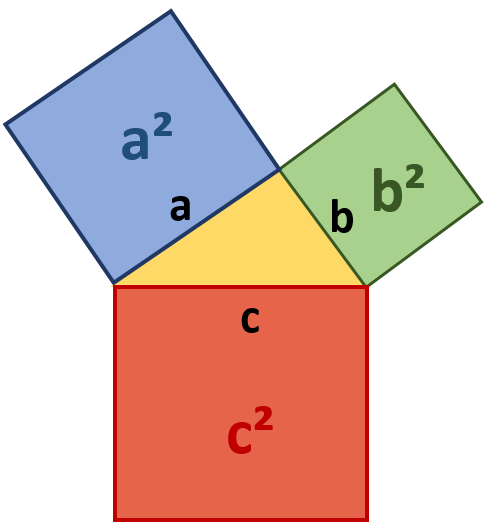
Der Satz des Pythagoras besagt:
Kathete² + Kathete²= Hypotenuse²
a² + b²= c²
Trigonometrie
Man unterscheidet die Ankathete und die Gegenkatheten.
- Die Gegenkatheten sind die Seiten, die dem gewählten Winkel gegenüberliegen.
- Als Ankatheten werden die andere, dem Winkel anliegende Kathete bezeichnet.
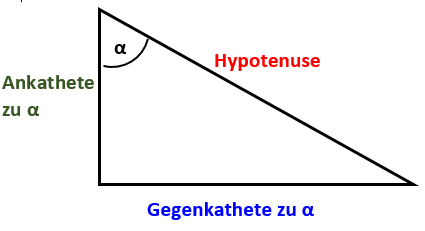
In einem rechtwinkligen Dreieck gilt:

Sinussatz
Der Sinussatz ist hingegen in jedem beliebigen Dreieck anwendbar. Dafür müssen allerdings
- eine Seite und zwei Winkel
oder - zwei Seiten und ein Winkel
gegeben sein.
Im zweiten Fall muss der Winkel einer der beiden gegebenen Seiten gegenüberliegen.
Der Sinussatz lautet:
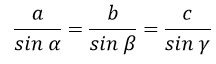
Wahrscheinlichkeitsrechnung
Ein Zufallsexperiment, bei dem alle Ergebnisse gleich wahrscheinlich sind, heißt Laplace-Experiment.
In diesem Fall kann man die Wahrscheinlichkeit P(E) so berechnen:
Wahrscheinlichkeit P(E) = Anzahl der zu E gehörenden Ergebnisse dividiert durch Anzahl aller möglichen Ergebnisse.
Beispiel
Wie groß ist die Wahrscheinlichkeit mit einem Würfel die Zahl 1 zu würfeln?
- Anzahl der möglichen Ergebnisse: 6
- Anzahl der zu E gehörenden Ergebnisse: 1
- Wahrscheinlichkeit = 1/6
Mehrstufige Zufallsexperimente
Mehrstufige Zufallsexperimente werden oft durch ein Baumdiagramm dargestellt. Für die Berechnung der Wahrscheinlichkeiten verwendet man folgende Regeln:
- Erste Pfadregel (Produktregel):
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis gehört. - Zweite Pfadregel (Summenregel):
Die Wahrscheinlichkeit eines (zusammengesetzten) Ereignisses ist gleich der Summe aller Wahrscheinlichkeiten der Pfade, die zu den Ereignissen führen.


